Model diagnostics in logistic regression

R
Published

June 19, 2025

Simulate some data

  • Idea:
    • Simulate some data with p numeric predictors
    • True relation for first predictor is quadratic, for all others true relation is linear
# Number of individuals:
n <- 1000 

# Number of parameters:
p <- 2

# matrix with predictors :
X1 <- matrix(rnorm(n * p), ncol = p)

# construct matrix, where first predictor is squarred, 
# so that a quadratic relation can be construted easily:
X2 <- X1
X2[, 1] <- X2[, 1] ^ 2

# beta consists just of ones:
beta <- rep(1, p)

# simulate outcome:
y_logit <- X2 %*% beta
p <- plogis(y_logit)
outcome <- rbinom(n, 1, p)

Fit a model

# fit a model with all predictors on linear scale:
fm_all_linear <- glm(outcome ~ X1, family = binomial())

# fit a model with first predictor quadratic:
fm_first_quadratic <- glm(outcome ~ X2, family = binomial())

Partial residual plots

# Function `prplot` slightly modified from package `faraway`:
prplot2 <- function (g, i) 
{
    xl <- attributes(g$terms)$term.labels[i]
    yl <- paste("beta*", xl, "+res", sep = "")
    x <- model.matrix(g)[, i + 1]
    y <- g$coeff[i + 1] * x + g$res
    tibble(x = x, y = y) |> 
      ggplot(aes(x, y)) + geom_point() + geom_smooth()
}
# If you fit the inadequate model with also a linear relation for the first 
# predictor, you see a characteristic pattern in the residuals:
prplot2(fm_all_linear, 1)
`geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'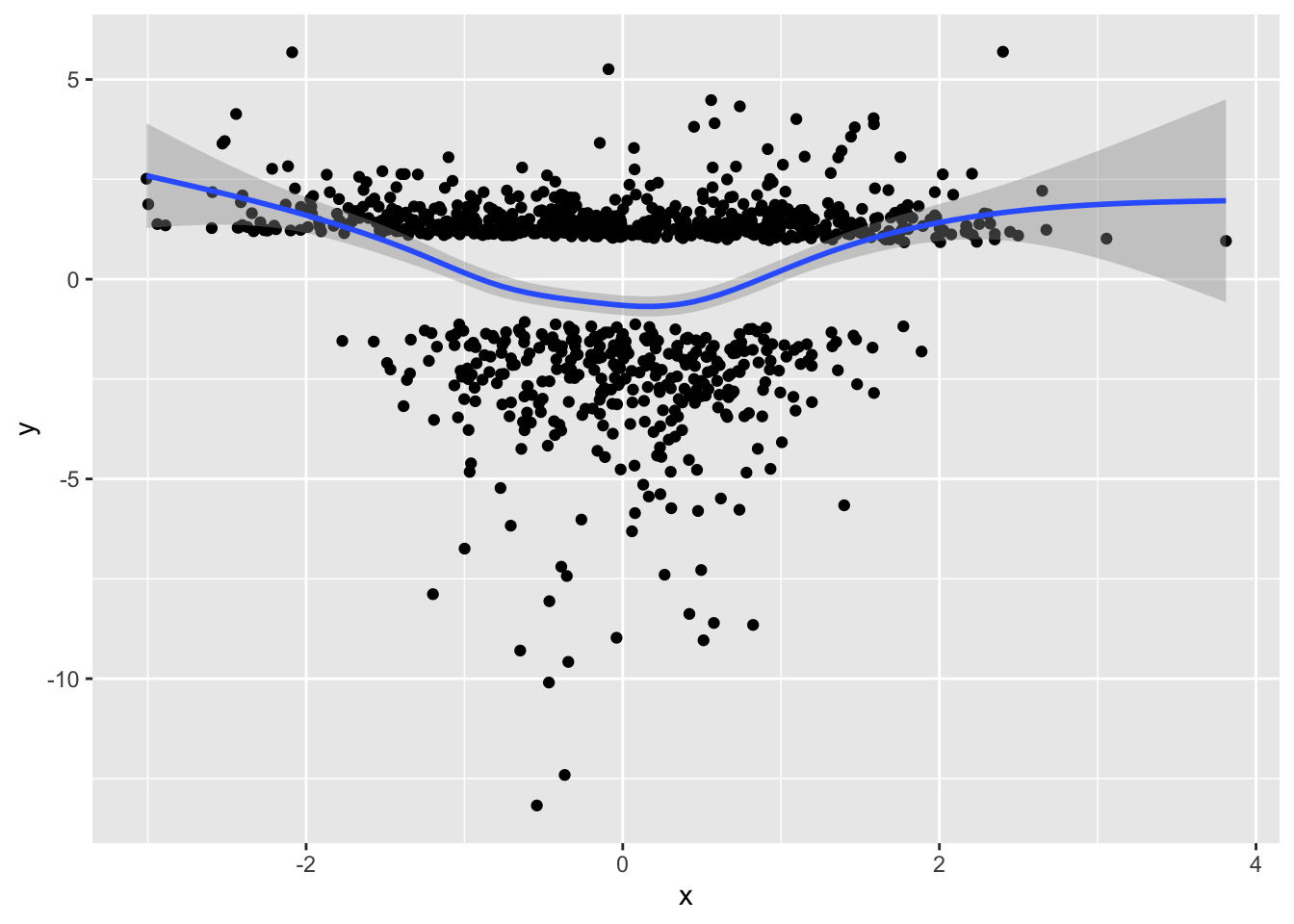

# If you fit the "true" model there is no such pattern:
prplot2(fm_first_quadratic, 1)
`geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'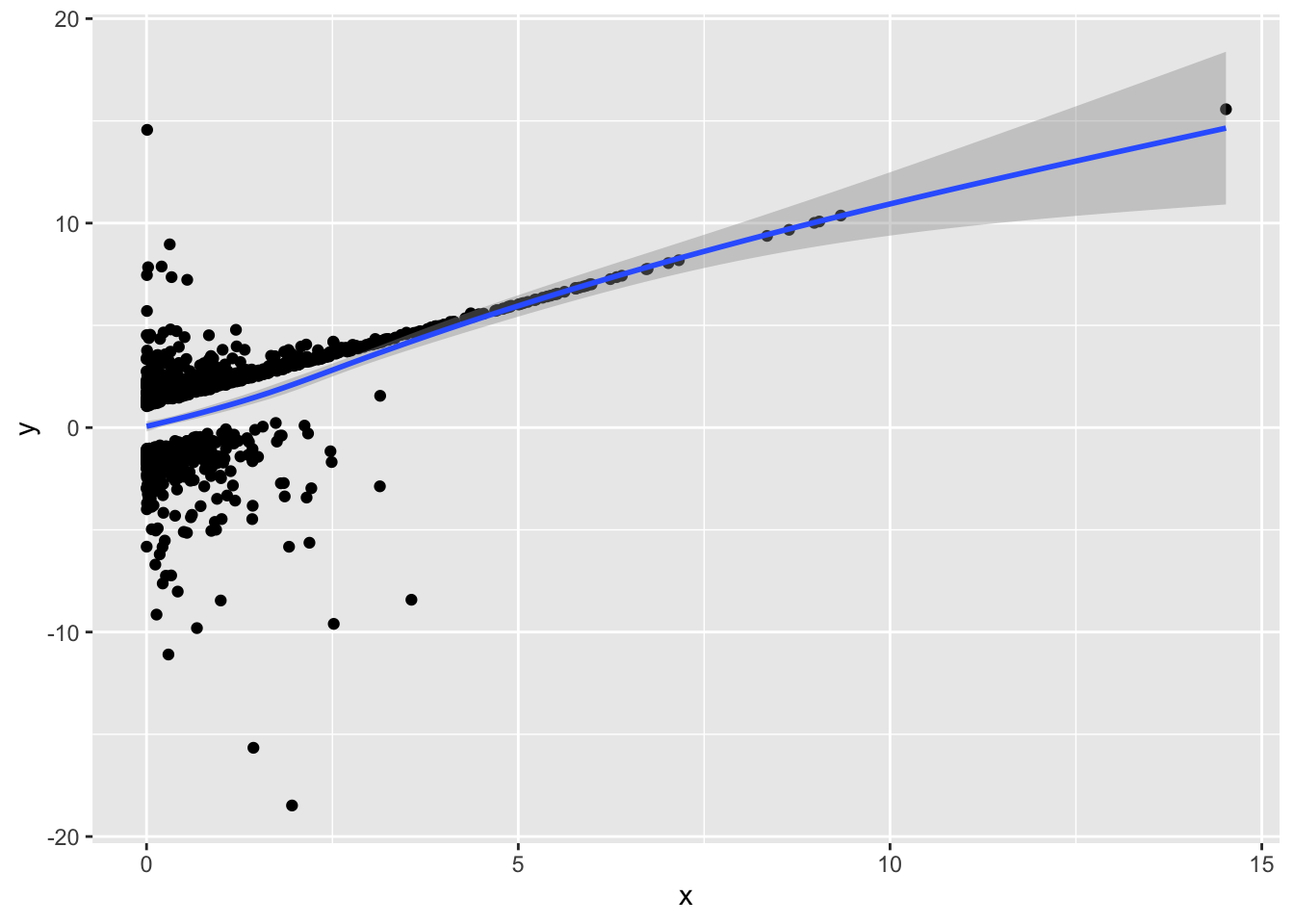

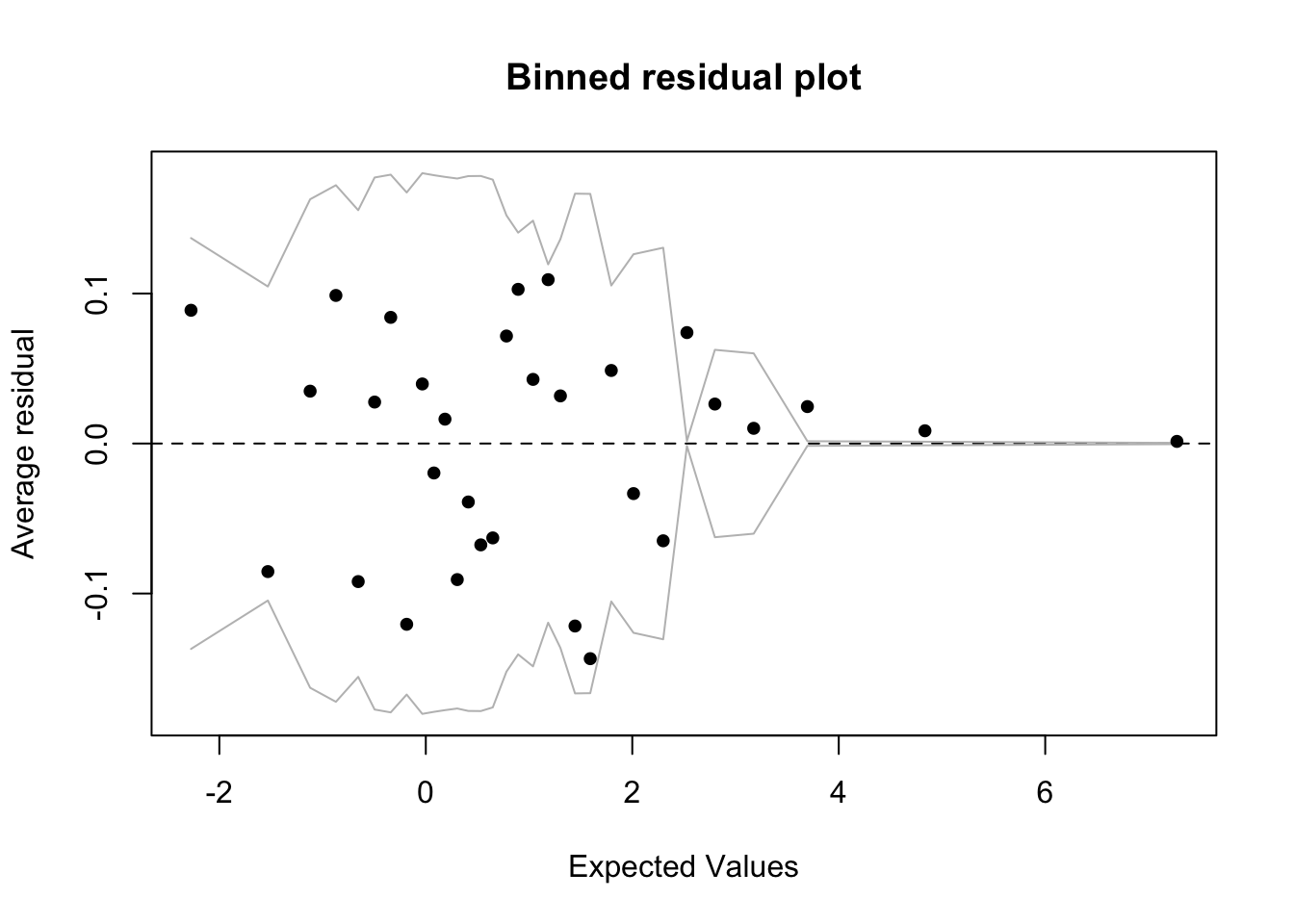
Binned plot

  • You can also see it via binnedplot:
library(arm)
Loading required package: MASS

Attaching package: 'MASS'
The following object is masked from 'package:dplyr':

    select
Loading required package: Matrix

Attaching package: 'Matrix'
The following objects are masked from 'package:tidyr':

    expand, pack, unpack
Loading required package: lme4

arm (Version 1.14-4, built: 2024-4-1)
Working directory is /Users/seb/Documents/Projects/00_websites/sbloggel/posts/2025-06-19-model-diagnostics-in-logistic-regression
binnedplot(predict(fm_all_linear), residuals(fm_all_linear, type = "response"))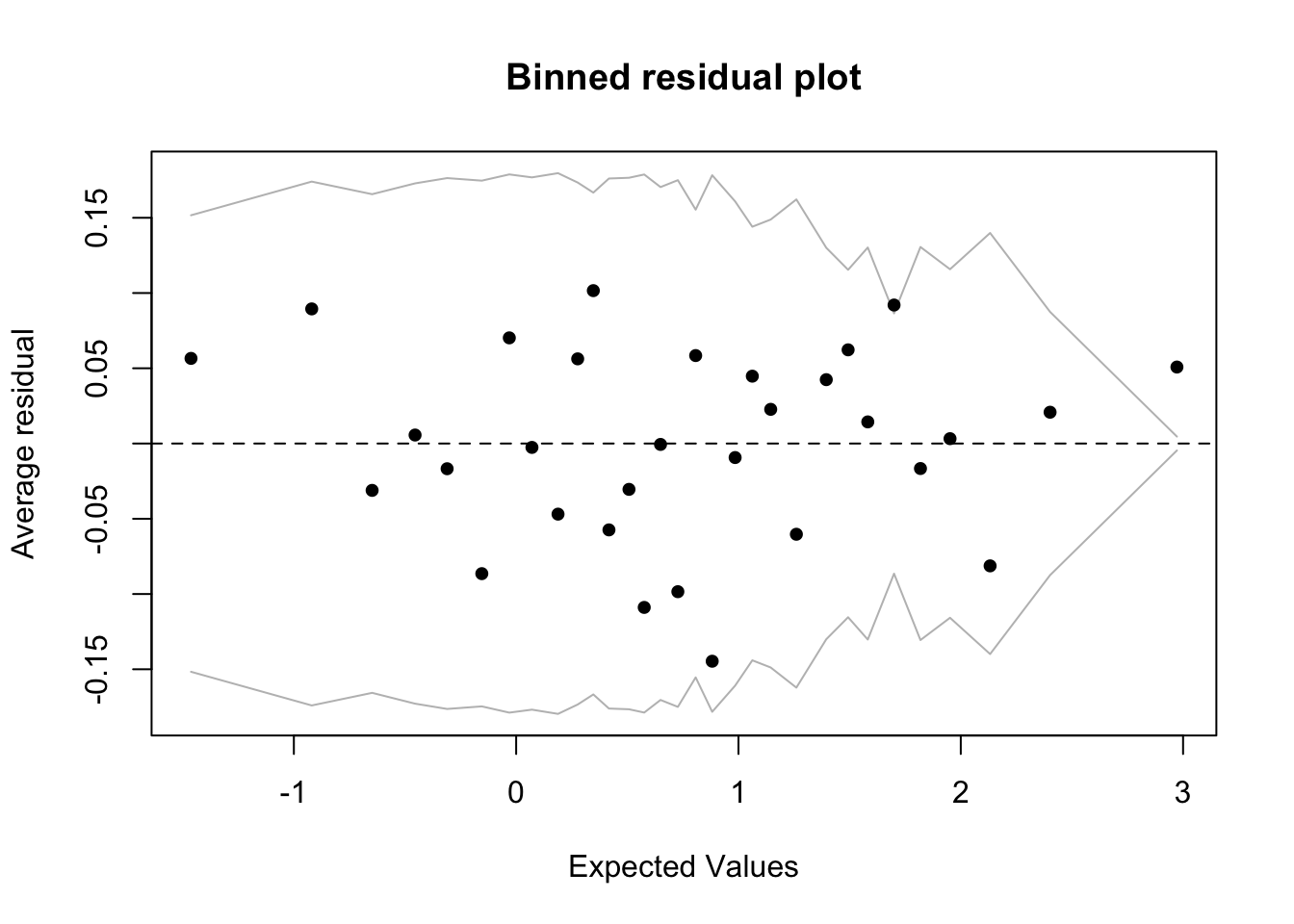

binnedplot(predict(fm_first_quadratic), residuals(fm_first_quadratic, type = "response"))