Understanding the multivariate normal distribution

library('tidyverse')
set.seed(1)

Link to question at stackexchange

Relations

n <- 1e4
x <- rnorm(n)
p_values <- pnorm(x)
plot(ecdf(p_values))
abline(0, 1, col = 'red', lty = 'dotted')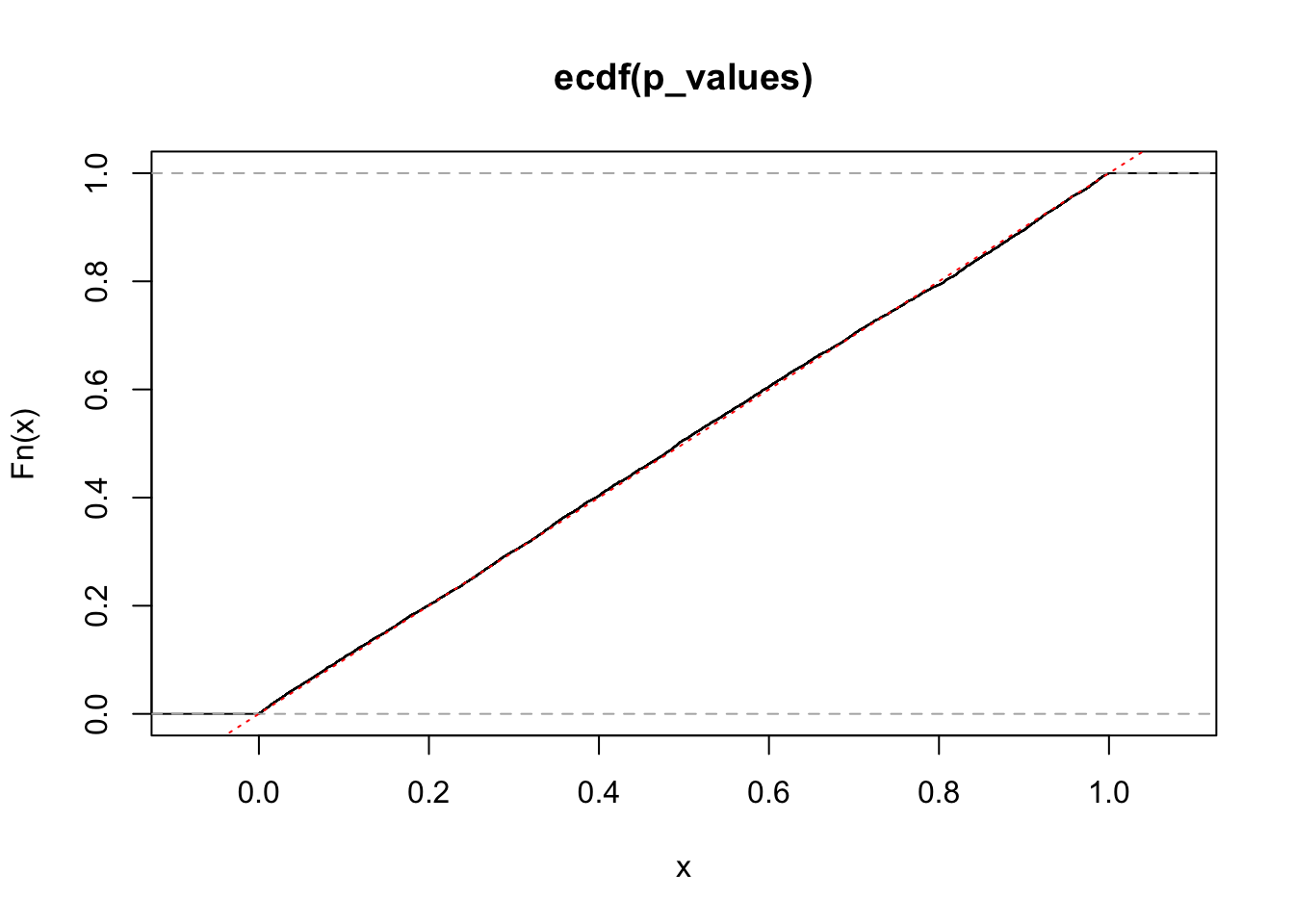

# help(package = 'mvtnorm')
# help(package = 'multcomp')

library('mvtnorm')
var_x1 <- 1
var_x2 <- 1
cov_x1_x2 <- 0.3
sigma <- cbind(c(var_x1, cov_x1_x2), c(cov_x1_x2, var_x2))
sigma

     [,1] [,2]
[1,]  1.0  0.3
[2,]  0.3  1.0

dat <- rmvnorm(n, mean = c(0, 0), sigma = sigma)


# calc_p <- function(x) {
#   pmvnorm(lower = -abs(x),
#           upper = abs(x),
#           sigma = sigma)
# }

calc_p <- function(x) {
  pmvnorm(lower = ifelse(x < 0, x, -Inf),
          upper = ifelse(x > 0, x, Inf),
          sigma = sigma)
}





# should be a straight line, but isn't - I don't understand why...
p_values <- apply(dat[1:min(n, 1e4), ], 1, calc_p)
plot(ecdf(p_values), xlim = c(0, 1))
abline(0, 1, col = 'red', lty = 'dotted')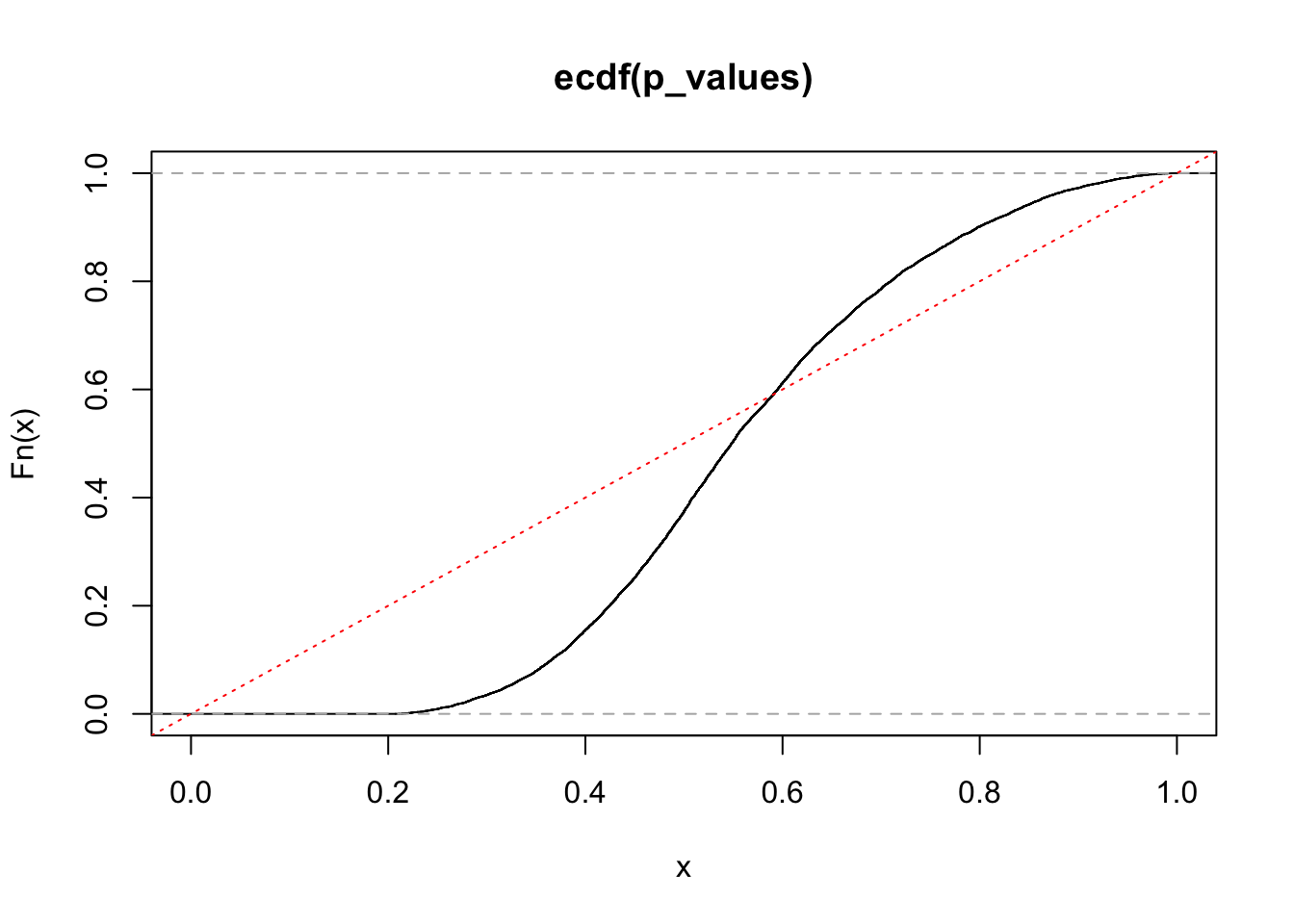

ii_1 <- dat[, 1] < qnorm(0.025, sd = sqrt(var_x1))
ii_2 <- dat[, 2] < qnorm(0.025, sd = sqrt(var_x2))

sum(ii_1)

[1] 229

sum(ii_2)

[1] 246

sum(ii_1 | ii_2)

[1] 457

sum(ii_1 & ii_2)

[1] 18