Gradient descent

library('tidyverse')
set.seed(1)

n <- 200
beta <- c(0.8, -0.3)
X <- matrix(nrow = n, ncol = length(beta), 
            data = rnorm(n * length(beta), 0, 4))

y <- X %*% beta + rnorm(n, 0, 3)

fm <- lm(y ~ X - 1)
summary(fm)

Call:
lm(formula = y ~ X - 1)

Residuals:
    Min      1Q  Median      3Q     Max 
-9.0310 -2.1055 -0.2301  1.9095 11.2183 

Coefficients:
   Estimate Std. Error t value Pr(>|t|)    
X1  0.85705    0.06124  13.995  < 2e-16 ***
X2 -0.32103    0.05629  -5.703 4.24e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.212 on 198 degrees of freedom
Multiple R-squared:  0.5391,    Adjusted R-squared:  0.5344 
F-statistic: 115.8 on 2 and 198 DF,  p-value: < 2.2e-16

calc_log_likelihood <- function(beta_1, beta_2) {
  beta_hat <- c(beta_1, beta_2)
  # print(beta_hat)
  # cat('\n')
  # return(NULL)
  y_hat <- X %*% beta_hat
  epsilon_hat <- y - y_hat 
  sigma_hat <- sd(epsilon_hat)
  dn <- dnorm(epsilon_hat, 0, sigma_hat, log = TRUE)
  return(sum(dn))
}

calc_log_likelihood(coef(fm)[1], coef(fm)[2])

[1] -516.1865

logLik(fm)

'log Lik.' -516.1859 (df=3)

dat <- expand_grid(beta_1 = seq(-5, 5, by = 0.1), 
                   beta_2 = seq(-5, 5, by = 0.1))

dat$loglik <- map2_dbl(dat$beta_1, dat$beta_2, calc_log_likelihood)

ii <- which.max(dat$loglik)

middle <- dat[ii, ]

dat |> 
  ggplot(aes(beta_1, beta_2, z = loglik)) + 
  geom_contour() + 
  geom_point(aes(x = middle$beta_1, 
                 y = middle$beta_2), 
             inherit.aes = FALSE)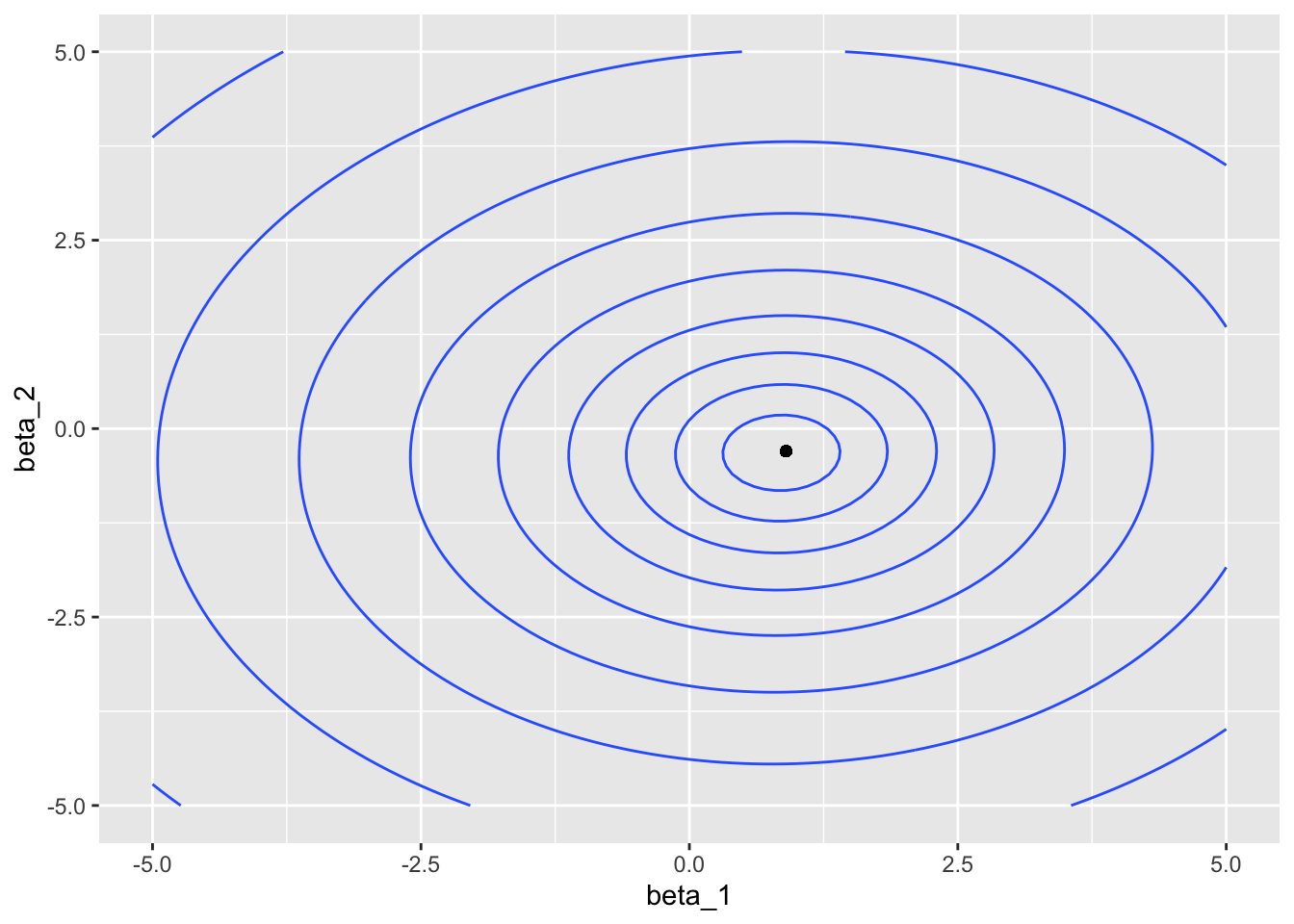

Example from r-bloggers

• Source: Link

attach(mtcars)

The following object is masked from package:ggplot2:

    mpg

gradientDesc <- function(x, y, learn_rate, conv_threshold, n, max_iter) {
  plot(x, y, col = "blue", pch = 20)
  m <- runif(1, 0, 1)
  c <- runif(1, 0, 1)
  yhat <- m * x + c
  MSE <- sum((y - yhat) ^ 2) / n
  converged = F
  iterations = 0
  while(converged == F) {
    ## Implement the gradient descent algorithm
    m_new <- m - learn_rate * ((1 / n) * (sum((yhat - y) * x)))
    c_new <- c - learn_rate * ((1 / n) * (sum(yhat - y)))
    m <- m_new
    c <- c_new
    yhat <- m * x + c
    MSE_new <- sum((y - yhat) ^ 2) / n
    if(MSE - MSE_new <= conv_threshold) {
      abline(c, m) 
      converged = T
      return(paste("Optimal intercept:", c, "Optimal slope:", m))
    }
    iterations = iterations + 1
    if(iterations > max_iter) { 
      abline(c, m) 
      converged = T
      return(paste("Optimal intercept:", c, "Optimal slope:", m))
    }
  }
}


# Run the function 

gradientDesc(disp, mpg, 0.0000293, 0.001, 32, 2500000)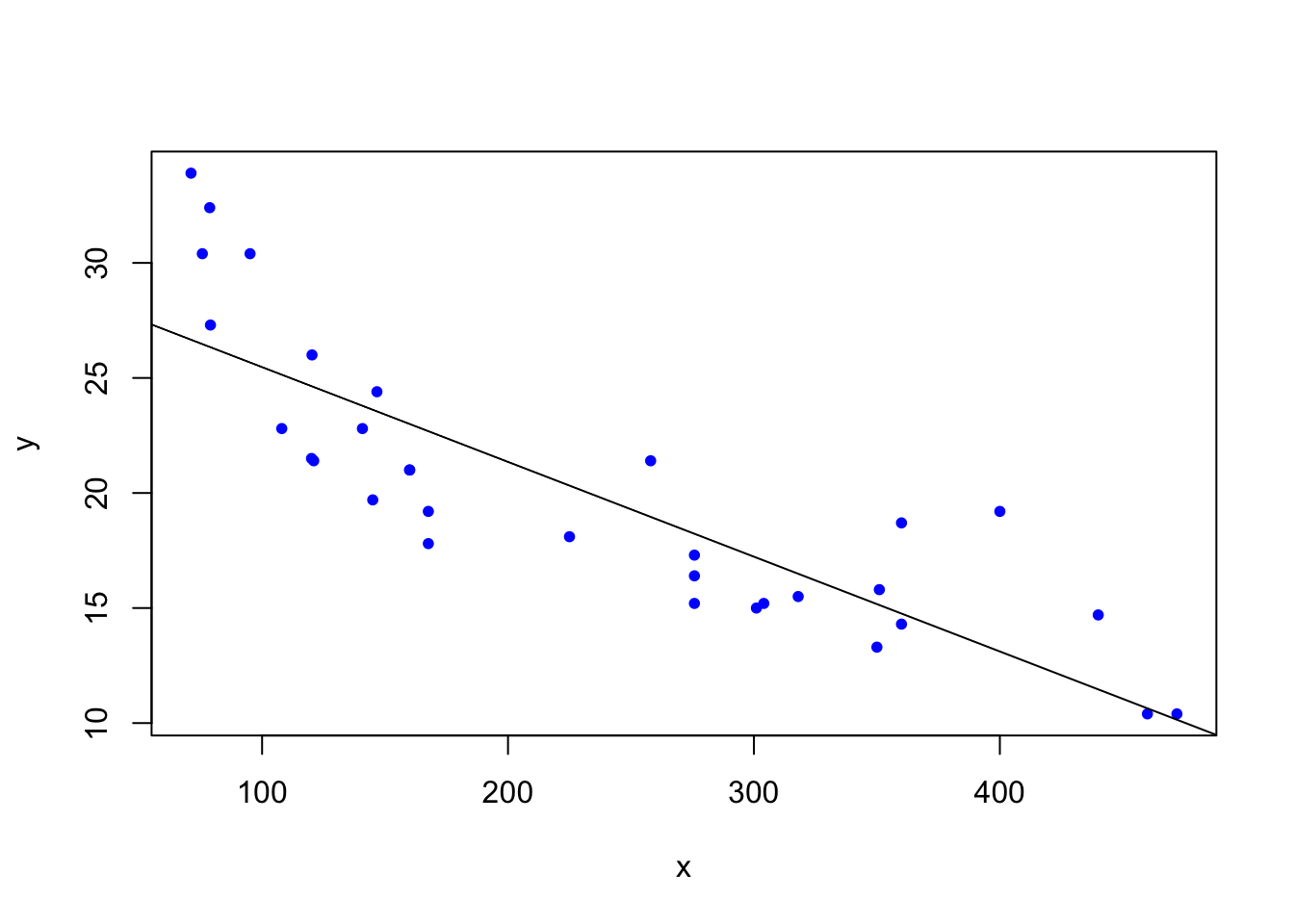

[1] "Optimal intercept: 29.5998515177117 Optimal slope: -0.0412151089930703"