SIRS model dynamics

Loading the required libraries

library('ggplot2')
library('tidyverse')
library('deSolve')
theme_set(theme_bw())

Simulate ODEs

sir_ode_deterministic <- function(t, state, pars) {
  with(as.list(c(state, pars)), {
    dS <- - beta * I * S + lambda * R
    dI <- beta * I * S - gamma * I
    dR <- gamma * I - lambda * R
    return(list(c(dS = dS, dI = dI, dR = dR)))
  }) 
}


infected_initial <- 0.5
initial_condition <- 
  c(S = 1 - infected_initial,
    I = infected_initial,
    R = 0)

step_length <- 1
max_time <- 100
timepoints <- seq(0, max_time, by = step_length)
grid_values <- 2^(-1:1)
grid_values <- 2^(-2:2)
grid_values <- 2^(-3:3)

result <- tibble()
for(beta in grid_values) {
  for(gamma in grid_values) {
    for(lambda in grid_values) {
      parameters <- list(beta = beta, 
                         gamma = gamma,
                         lambda = lambda)
      solution <- ode(y = initial_condition, 
                      times = timepoints,
                      func = sir_ode_deterministic,
                      parms = parameters) %>% 
        unclass %>% as_tibble
      solution$beta <- beta
      solution$gamma <- gamma
      solution$lambda <- lambda
      result <- rbind(result, solution)
    }
  }
}

result <- pivot_longer(result, cols = c('S', 'I', 'R'))

last <- result %>% 
  filter(time == max_time) %>% 
  mutate(name = factor(name, levels = c('S', 'I', 'R')))

last %>%
  ggplot(aes(beta, value, colour = name)) + 
  geom_point() + geom_line() +
  facet_grid(rows = vars(gamma), 
             cols = vars(lambda), 
             labeller = label_both) +
  labs(xlab = 'beta', ylab = 'Fraction', colour = 'Compartment') +
  scale_x_continuous(trans='log10')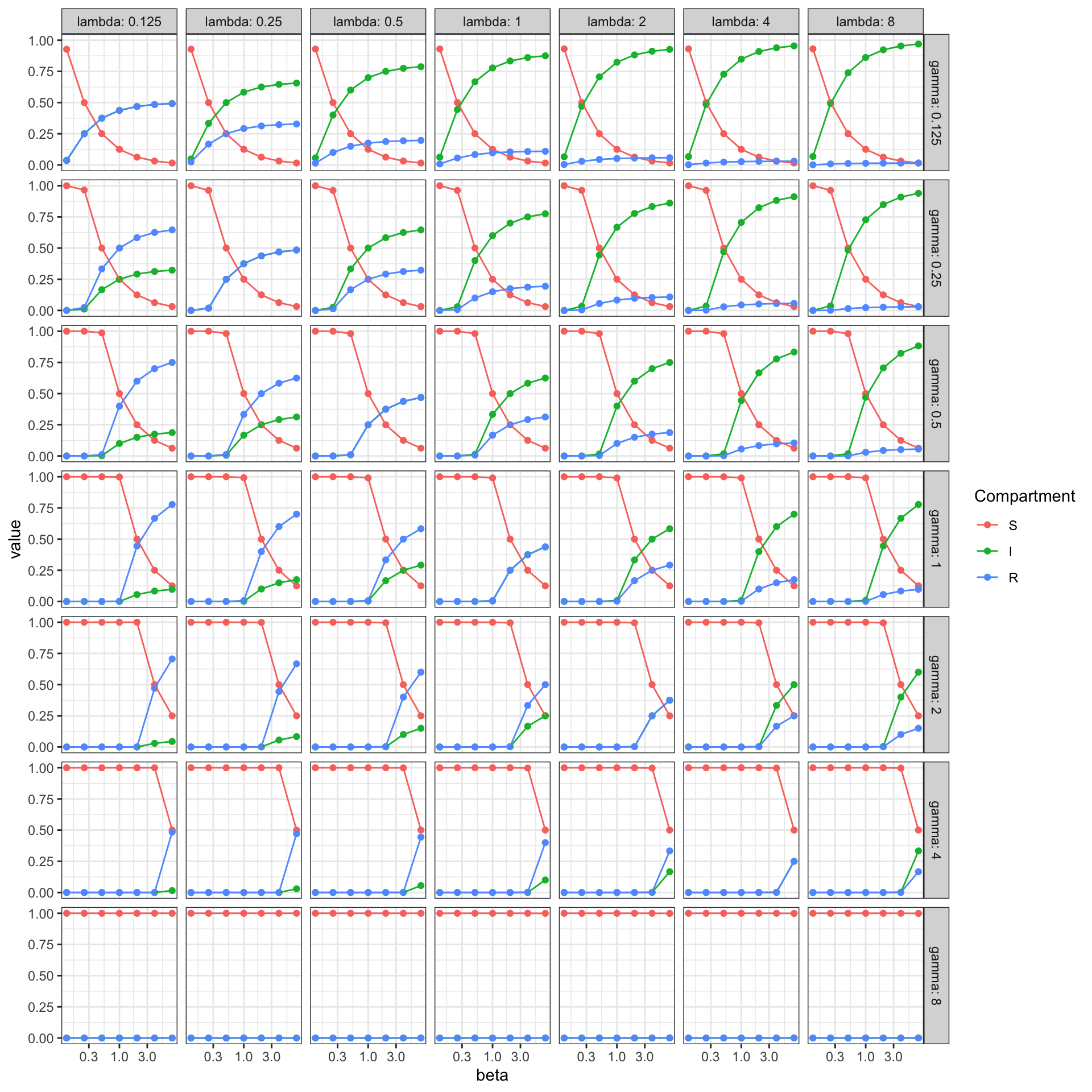

last %>%
  ggplot(aes(x = beta, y = value, fill = name)) +
  geom_area() +
  facet_grid(rows = vars(gamma), 
             cols = vars(lambda), 
             labeller = label_both) +
  labs(xlab = 'beta', ylab = 'Fraction', fill = 'Compartment') +
  scale_x_continuous(trans='log10')

ss <- last %>% 
  group_by(beta, gamma, lambda) %>% 
  summarise(ss = sum(value))

`summarise()` has grouped output by 'beta', 'gamma'. You can override using the
`.groups` argument.

Analytical approach

Solution in terms of parameters in red.

Equilibrium conditions

$$\begin{array}{rlr}1& =S+I+R& (1)\\ 0& =-\beta IS+\lambda R& (2)\\ 0& =\beta IS-\gamma I& (3)\\ 0& =\gamma I-\lambda R& (4)\end{array}$$

Algebraic transformation

$$\begin{array}{rlr}R& =1-S-I& (1b)\\ S& =\gamma /\beta & (3b)\end{array}$$

Plugging in

$$\begin{array}{rlr}(3b)\to (2):I& =\lambda /\gamma R& (5)\\ (1b)\to (5):I& =\frac{\lambda (\beta -\gamma )}{\beta (\gamma +\lambda )}& (6)\\ (3b)+(6)\to (1b):R& =\frac{\gamma (\beta -\gamma )}{\beta (\gamma +\lambda )}& (7)\end{array}$$

Plots

last_w <- pivot_wider(last, names_from = name, values_from = value)
last_w$S_calc <- pmin(1, last_w$gamma / last_w$beta)
last_w$I_calc <- 
  pmax(0, pmin(1, with(last_w, (lambda * (beta - gamma))) / 
                 (beta * (gamma + lambda))))
last_w$R_calc <- 
  pmax(0, pmin(1, with(last_w, (gamma * (beta - gamma)) / 
                         (beta * (gamma + lambda)))))

last_w$I_calc <- 1 - last_w$S_calc - last_w$R_calc

last <- last_w %>% 
  pivot_longer(cols = c('S_calc', 'I_calc', 'R_calc'))


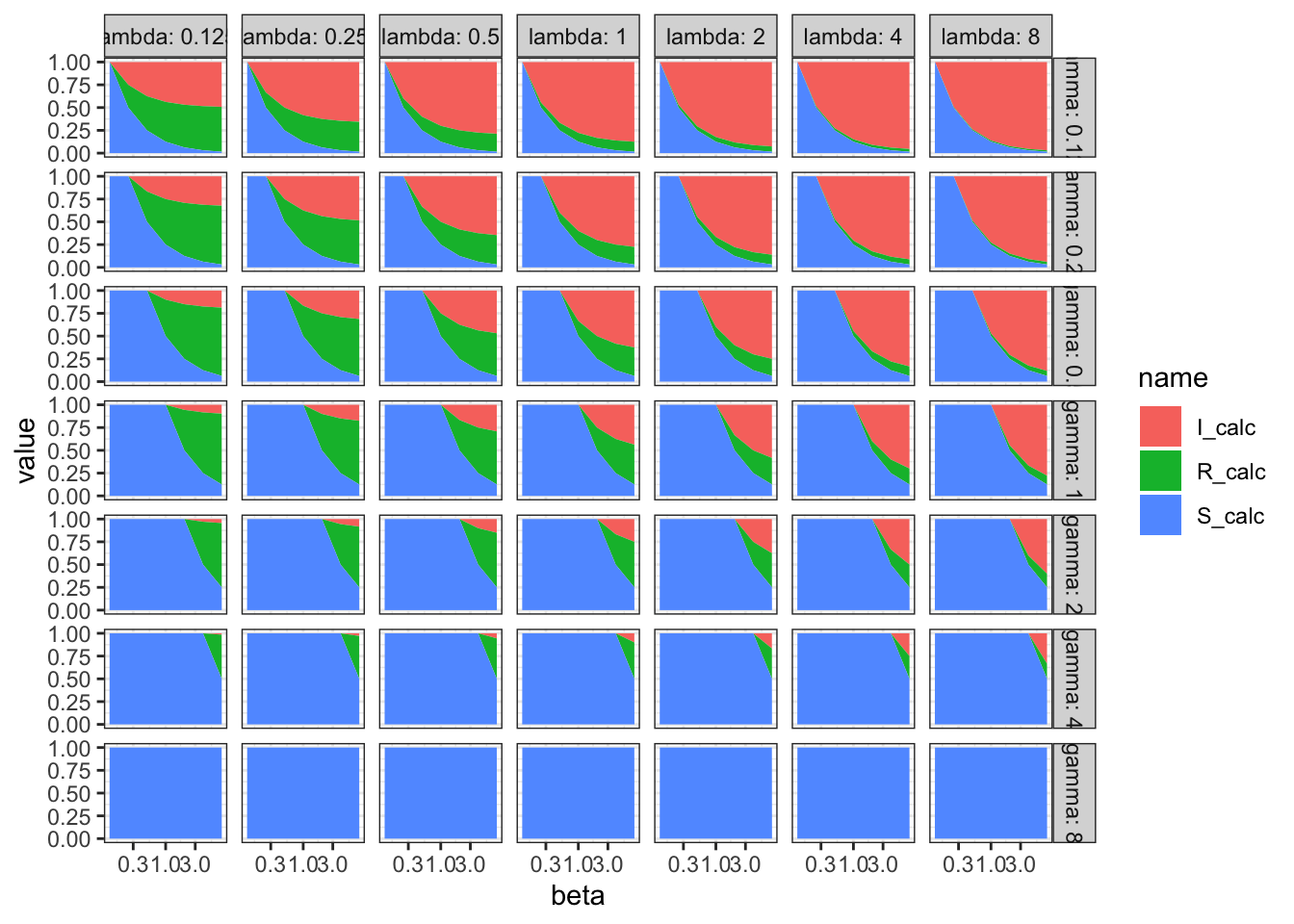
last %>%
  ggplot(aes(x = beta, y = value, fill = name)) + 
  geom_area() +
  facet_grid(rows = vars(gamma), 
             cols = vars(lambda), 
             labeller = label_both) +
  labs(ylab = 'Fraction',  xlab = 'beta', colour = 'Compartment') +
  scale_x_continuous(trans='log10')